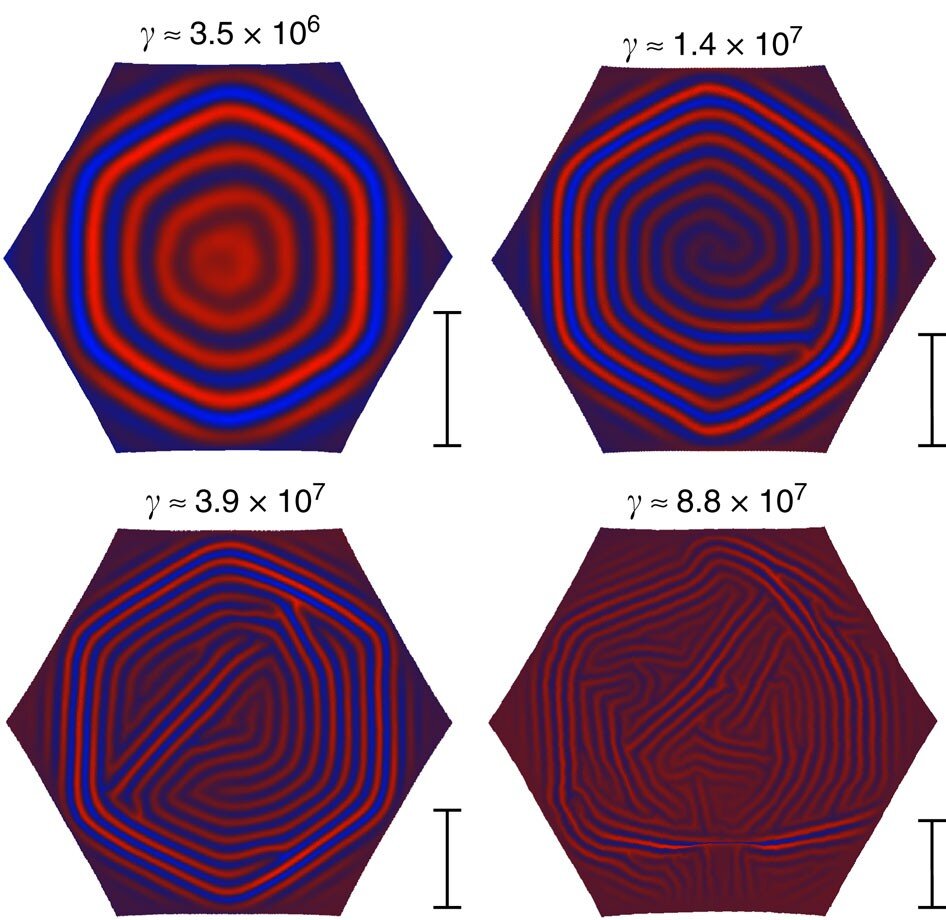
Escalado de tamaño de dominio. Patrones típicos de arrugas en equilibrio en una sección hexagonal de una capa esférica delgada sobre un sustrato líquido. Todos los parámetros de simulación se mantienen fijos, excepto el espesor de la hoja. El número de Föppl-von Kármán γ del sistema se indica encima de cada patrón. Si bien el patrón superior izquierdo está claramente dividido en seis dominios, el aumento de γ parece disminuir el tamaño típico del dominio. La barra de escala a la derecha de cada patrón muestra la escala de los tamaños de dominio típicos predichos por la ecuación (20), hasta un factor constante (solo las proporciones entre barras son significativas ya que la ecuación (20) sugiere solo la escala del tamaño típico y deja el prefactor desconocido). Crédito: Comunicaciones de la naturaleza (2017). DOI: 10.1038/ncomms15809
Un objeto que es intrínsecamente plano, digamos un trozo de papel, se puede moldear en un cilindro sin estirarlo ni rasgarlo. Sin embargo, no ocurre lo mismo con algo intrínsecamente curvo como una lente de contacto. Cuando se comprimen entre dos superficies planas o se colocan sobre el agua, los objetos curvos se aplanarán, pero con arrugas que se forman a medida que se doblan.
Ahora, una investigación de la Universidad de Pensilvania, la Universidad de Illinois Chicago (UIC) y la Universidad de Syracuse ha demostrado que con una geometría simple es posible predecir los patrones de esas arrugas, tanto dónde se formarán como, en algunos casos, su dirección. Los hallazgos, publicados en Física de la naturalezatienen una variedad de implicaciones, desde cómo los materiales interactúan con la humedad y reflejan la luz solar en la naturaleza hasta la forma en que un dispositivo electrónico flexible podría doblarse.
«La belleza de este trabajo es lo simple que realmente es», dice Eleni Katifori, profesora asociada en el Departamento de Física y Astronomía de Penn. «Lo que hay detrás es muy complicado, la física que se traduce a través de estas reglas que encontramos, pero las reglas en sí mismas son muy simples. Es inspirador».
Reunión de las mentes
Desde su Ph.D. trabajo, Katifori se ha interesado en la mecánica de cómo se curvan las membranas delgadas. Aunque esto siguió siendo una curiosidad, su camino de investigación se desvió hacia las redes de flujo de fluidos. Luego, mientras colaboraba en un proyecto con el colega de Penn Randall Kamien y luego con el becario postdoctoral Hillel Aharoni, Katifori observó algo que no podía explicar en ese momento. «Es decir, notamos que se forman arrugas en los dominios», dice ella.
En otras palabras, cuando una superficie curva se aplana, termina con un exceso de material y las consiguientes arrugas. Esas arrugas emergen en patrones o sectores. «La pregunta fue, ¿por qué las arrugas se organizan de esa manera?» dice Katifori. «No entendíamos cuán importantes son realmente los dominios en las arrugas».
En una conferencia en 2016, el matemático Ian Tobasco, profesor asistente en la UIC, escuchó a Aharoni dar una charla sobre el tema. «Fue la primera vez que vi que se presentaba este sistema modelo», dice Tobasco. «Pensé que era realmente genial.» A mediados de 2017, Katifori, Aharoni y sus colegas publicaron hallazgos sobre el tema en Comunicaciones de la naturalezaLuego, en un taller más tarde ese año, Tobasco conoció a Joseph Paulsen de Syracuse, quien había presentado datos preliminares sobre la experimentación que su grupo había realizado sobre las arrugas.
A principios de 2018, Tobasco comenzó a trabajar en serio en una teoría matemática para las arrugas y durante el almuerzo en una conferencia ese verano, Katifori, Tobasco y Paulsen acordaron que compartían el interés en este problema. Decidieron colaborar, centrándose en analizar cuánto la forma física del material y la curvatura de la que parte podrían afectar a los patrones de arrugas.
Trabajando a través del problema
Para algunos fondos, la curvatura puede ser positiva, como la redondez de una pelota de béisbol o un globo terráqueo, o negativa, como la silla de montar de un caballo o el lugar en una botella de vidrio donde el cuello se encuentra con la base. También hay material plano, como una hoja de papel.
En este trabajo, los investigadores se centraron en conchas curvadas positiva y negativamente.
De cada uno, luego quitaron formas básicas, como triángulos, cuadrados y óvalos. «Piense en un cortador de galletas. Digamos que tomo un objeto con una curvatura positiva o negativa, luego corto una de estas formas y la coloco sobre un líquido», dice Katifori. ¿Sería posible adivinar los patrones de las arrugas y calcular la dirección en que fluirían las arrugas? Para cada forma, Tobasco resolvía la teoría basándose en los principios fundamentales que había elaborado y publicado, y luego proponía predicciones.
Con base en esos hallazgos, Katifori y la investigadora postdoctoral de Penn, Desislava Todorova, realizaron simulaciones, ingresando formas y parámetros individuales en un programa de computadora. Un trabajo similar estaba ocurriendo en el laboratorio dirigido por Paulsen, profesor asistente de física en Syracuse, a través de experimentos que estaba realizando en una película de poliestireno 1000 veces más delgada que una hoja de papel. «Está hecho del mismo material que los cacahuetes de embalaje», dice Tobasco, «pero en lugar de la forma tridimensional de un cacahuete de embalaje, imagina que es plano como una hoja».
A través de las simulaciones, la experimentación y muchas idas y venidas para refinar el proceso y expandir la teoría original, el trío comenzó a discernir que al aplicar principios geométricos directos, podían saber de antemano qué patrón tomarían las arrugas y para un subconjunto. —lo que describen como arrugas «ordenadas»— en qué dirección correrían.
Los principios geométricos
Para explicar uno de esos principios, Katifori usa un polígono de cinco lados. «Primero inscribo un círculo en el polígono», dice ella. «Los puntos donde ese círculo toca los bordes del polígono determinan dónde dibujo mis líneas». Hace una pausa para crear una segunda forma dentro de la primera, esta con cuatro lados desiguales; comienza cada línea donde se unen el círculo y el polígono exterior, conectando las cuatro líneas interiores. «Ahora tengo uno, dos, tres, cuatro, cinco dominios», continúa, señalando el quinteto de secciones recién acordonadas.
Para formas simples como esta, las secciones exteriores contendrán arrugas ordenadas, que están organizadas y ordenadas, siguiendo la dirección de las líneas interiores que dibujó Katifori. Dentro del nuevo polígono interior, todavía se forman arrugas, pero siguen siendo desordenadas e impredecibles.
Tobasco señala otro ejemplo, uno que determinó que era universalmente cierto para formas cortadas de conchas con curvas negativas. «Al final, es muy sencillo predecir los patrones de arrugas. Todo lo que tiene que hacer es dibujar segmentos de línea que se encuentren con el límite en ángulo recto». En otras palabras, comience en un punto dentro de la forma y cree una línea directa hasta el borde de la forma, pero solo en un punto donde se formará un ángulo recto.
Eso tomó un año para que el equipo lo entendiera. «Las ecuaciones que determinan el diseño de las arrugas son terribles de resolver, y muchos de los patrones que observamos en nuestros experimentos y simulaciones son bastante complicados», dice Paulsen. «Pero resulta que bajo un determinado conjunto de condiciones, se puede predecir el diseño de las arrugas con un conjunto simple de reglas. Eso significa que ahora tenemos una forma rápida y eficiente de diseñar patrones de arrugas».
«Su simplicidad es hermosa y también es útil», agrega, particularmente para superficies arrugadas que cumplen una función como permitir la adhesión o el flujo de fluidos.
Katifori menciona ejemplos similares. «Digamos que hay humedad o humedad en el aire. El agua se comportará de manera diferente en los valles y las colinas de una superficie acanalada», dice ella. «Al controlar el patrón de arrugas, tal vez pueda afectar la forma en que se condensará el agua».
Que viene despues
Los investigadores todavía tienen más que entender sobre estas superficies texturizadas complejas, como cómo extraer patrones de arrugas desordenadas, por qué los dominios ordenados y desordenados pueden coexistir, y por qué hay una «reciprocidad» que vincula capas curvas negativas y positivas, lo que significa que una vez que el patrón para uno está determinado, es sencillo predecir el patrón para el otro.
Por ahora, sin embargo, dicen que están entusiasmados con el potencial de lo que han aprendido hasta este punto.
«Tienes una teoría complicada que, al final del día, se reduce a matemáticas relativamente simples que casi cualquiera puede hacer con un compás y una regla», dice Katifori. «Es una solución elegante y hermosa para un problema complejo».
Uso de pruebas matemáticas, experimentos y simulaciones para mostrar cómo se arruga un material cuando se aplana
Ian Tobasco et al, Soluciones exactas para los patrones de arrugas de cubiertas elásticas confinadas, Física de la naturaleza (2022). DOI: 10.1038/s41567-022-01672-2
Citación: Cuando los materiales curvos se aplanan, la geometría simple puede predecir los patrones de arrugas que emergen (11 de septiembre de 2022) consultado el 12 de septiembre de 2022 en https://phys.org/news/2022-09-materials-flatten-simple-geometry-ruga. html
Este documento está sujeto a derechos de autor. Aparte de cualquier trato justo con fines de estudio o investigación privados, ninguna parte puede reproducirse sin el permiso por escrito. El contenido se proporciona únicamente con fines informativos.